在前面的資料庫文章裡曾介紹過 B-tree,一種平衡的搜尋樹,利用樹狀的結構來達成快速尋找的目的,而且因為是平衡的,所以從 root 出發到每一個樹葉的尋找成本是一樣的,這也是必要的,畢竟資料庫引擎用公平的方式來對待所有的資料.然而,B-tree 的結構並非是 binary 的型式,因此這帶給它很大的彈性可以方便地達成一個完全平衡的狀態.在前幾篇的文章也談過了 binary search tree,若你看過的話,你會清楚地知道 binary search tree 和 binary tree 的不同.在 binary search tree 裡,因為在建立樹的過程中有一個很重要的特性,就是右邊子節點的值大於父節點,左邊子節點的值小於父節點,因此在建立樹或是尋找節點時,到達一個節點時,只需要選擇其中一邊,不是左邊就是右邊,所以也達到 "binary search" 的效果.如前面的文章所說,binary search tree 的特性並不保證樹結構本身是平衡的,所謂的平衡就是其結構會和 complete binary tree 很接近.因為 binary search tree 沒有這樣的特性,因此樹的結構很可能是 "歪" 的.
為了要防止這種 "歪" 的情況,在早期的電腦科學研究裡便出現了許多的點子和做法,其中一個稱為 AVL Tree.這是兩位前蘇聯時代的科學家所發明的方法.發明的時間都是在我們出生之前 (我猜想這部落格的讀者群應該沒人超過 60 歲).首先,先把 AVL tree 的時間複雜度列出來.
Search: O(log n), Insert: O(log n), Delete: O(log n),不論是 average case 或是 worst case 都是一樣的時間複雜度,超級完美的.這也是為什麼在上一篇章的 APCS 考題會拿像 binary search tree 的實做來用,因為就是這麼快.不論是刪除或插入,甚至尋找都是 O(log n),為什麼可以這麼快呢? 接下來將來說重點了.
AVL Tree 是一種 binary search tree 的特例,所謂的特例是指 binary search tree 再加上一些其他的特性之後就能變成 AVL tree.而這一個特性稱為 balance factor.每一個節點上都會有一個 balance factor,它代表的是一個值,其值是右邊子樹的高度減掉左邊子樹的高度.例如:
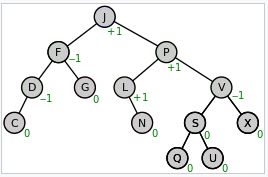
source: Wikipedia
節點 F ,右邊高度為 1,左邊高度為 2,所以 F 節點的 balance factor 為 1 -2 = -1,其他的節點也是用同樣的公式而得.AVL tree 定義了每個節點的 balance factor 必須為 -1 , 0 或 1.透過 balance factor 的限制,我們能知道這一個樹就 "比較" 不會那麼歪掉了,因為右邊子樹和左邊子樹的高度最多只能相差 1 而己.為了確保這個特性能發生,在插入節點或刪除節點的過程裡便需要採取一些動作.而這些動作如下:
1. 往左轉
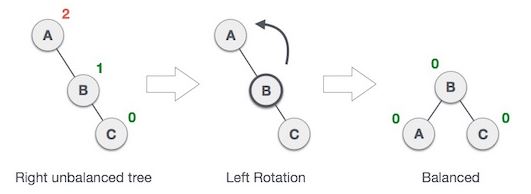
source: www.tutorialspoint.com
如上圖,節點 A 的 balance factor 是 2,因此必須降低它,由於這是 binary search tree,所以 C 的值大於 B,而 B 的值又大於 A,因此,要把樹技折下來的話,拿中間者來當新的父節點最好,於是以 B 為中心將 A 往左轉,所以就變成了最右邊的圖,這樣就符合了 AVL tree 的特性.
2. 往右轉
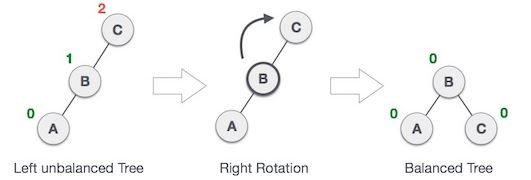
source: www.tutorialspoint.com
往右轉的情況剛好是和第一種相似,只是換另一邊而己.
3. 往左再右
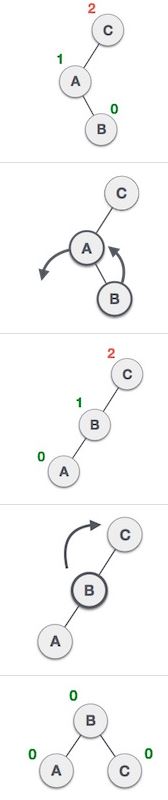
source: www.tutorialspoint.com
第三種情況其實是前面兩種情況的綜合體.若你看懂前面兩個為何要那樣轉的話,我相信你也一定看的懂第三種.其主要目的就是要讓 AVL tree 的特性可以滿足.
最後第四種,可想而知就是往右再往左.
4. 往右再往左
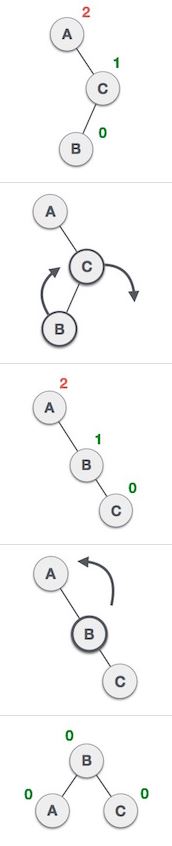
source: www.tutorialspoint.com
第四種情況就是第三種的另外一邊.只要你懂第三種情況,那麼第四種情況自然也不會是問題.
你可能會問我,像這種 AVL tree 要應用在什麼地方.老實說,到處都是,許多程式語言在他們的 standard libary/SDK 裡都會提供這種平衡的 binary search tree.我在工作上時常會用到這類型的資料結構以快速建立資料和尋找資料.前一篇 APCS 的解題就是靠類似 AVL tree 這種的平衡樹才能將時間複雜度降到 O(n log n).別以為 O(n2) 和 O(n log n) 相差不多,一旦輸入的數量到達數以萬計時,你的家用 CPU 就會告訴你他們之間有很大的差距了.
在 Wikipedia 上你也可以找到一個
動態的圖來說明 AVL tree 在建立的過程中,這些節點是如何左轉或右轉來達成平衡.AVL tree 將達成平衡這件事分攤在節點插入和刪除的過程中,因為才使得插入節點,刪除節點和尋找節點都有相同的時間複雜度.這的確是很高明的做法,我們大家又再一次站在巨人的肩膀上來看見電腦科學的神奇之處.